幅優先探索――グラフ探索
では、ここからアルゴリズムを紹介していきましょう。最初に紹介するのはグラフを探索するアルゴリズムの「幅優先探索」です。
そもそもコンピューターサイエンスでいうグラフとは、複数個の頂点(ノード)が辺で結ばれたものをいいます。人間関係(ソーシャルグラフ)、路線図、コンピューターネットワークなど、様々なものをグラフで表現できます。
これらのグラフを探索するためのアルゴリズムの一つである幅優先探索は、全貌のわからないグラフにおいて、始点から辺を辿りながら頂点を探索し、指定された頂点(ゴール)に辿り着けば目的達成です。端的には、頂点を探索する際、始点に近い頂点から優先的に探索していくアルゴリズムです。
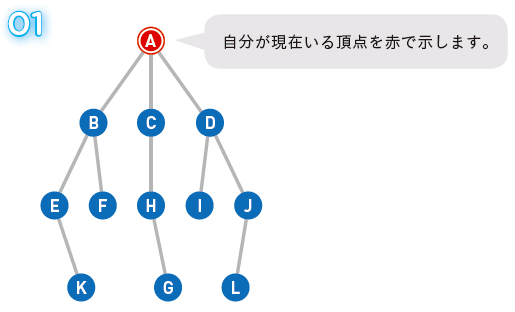
まず、始点を定めましょう。今回はAです。ゴールとしてGを設定しますが、Gがどこにあるかは最初の時点ではわかりません。
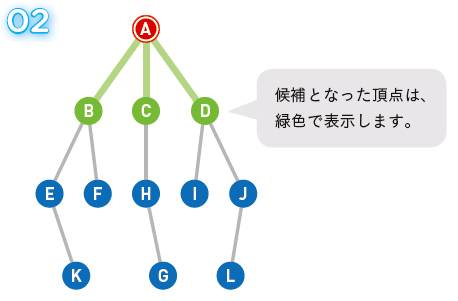
Aから辿れる頂点B、C、Dが次に進む頂点の候補です。
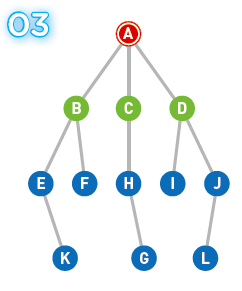
候補の中から頂点を一つ選びます。選択の基準は、最も早く候補に追加されたものです(同じタイミングのときはどれでも構いません)。
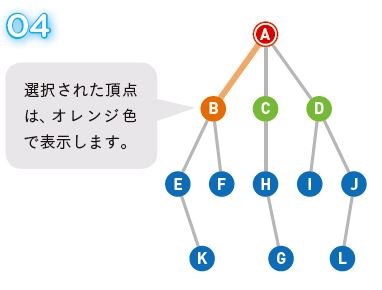
今回はB、C、Dが同じタイミングで候補となったのでBを選択します。
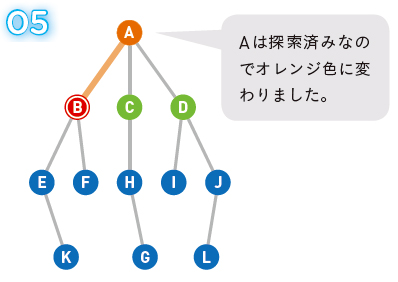
Bに移動すると、Aが探索済みとなります。

Bから辿れるEとFを候補に追加しましょう。これで候補がC、D、E、Fとなりました。
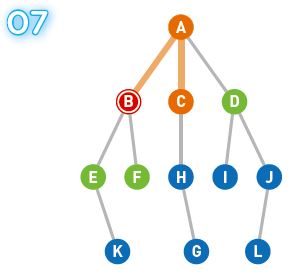
C、D、E、Fのうち、最も早く候補になったのはCとDです。今回も左側のCを選択します。
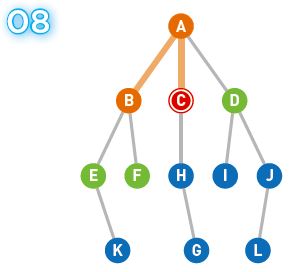
Bから、選択したCに移動します。Bが探索済みとなります。
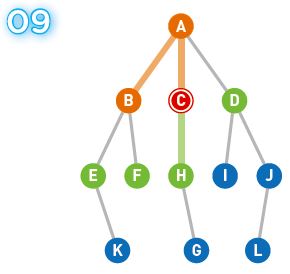
Cから辿れるHが新たに候補に加わります。現在の候補はD、E、F、Hです。
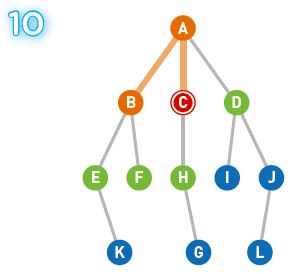
このように、ゴールに辿り着くか、すべての頂点を探索し終えるまで探索を繰り返します。
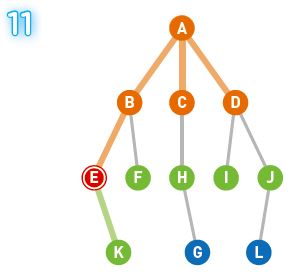
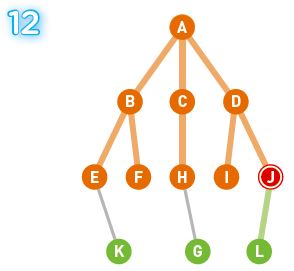
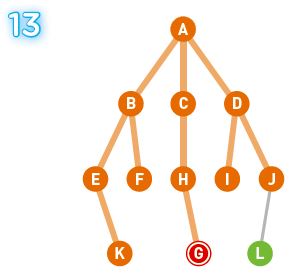
今回の例での選択順はA、B、C、D、E、F、H、I、J、K、そしてGとなりました。
幅優先探索では文字どおり幅広く探索を行っていく特徴があります。当たり前のことですが、始点の近くにゴールがあるほうが探索が早く終了します。
ちなみに、ここまで例として用いてきた連結して閉路のないグラフは木と呼ばれています。また、始点と終点が同じ頂点である(閉路がある)グラフも同様に探索することができます。


