アルファ碁ゼロにおけるディープラーニング
アルファ碁ゼロでは、従来版アルファ碁における次の一手予測をつかさどるポリシーネットワークと、勝率予測をつかさどるバリューネットワークとを統合したディープラーニングモデルが用いられます。2017年度版の新しいネイチャー論文(MEMO参照)では、このネットワークをdualと言及しているため、本章ではデュアルネットワークと呼ぶことにします。
本節では、アルファ碁ゼロのデュアルネットワークと、従来版アルファ碁のポリシーネットワーク・バリューネットワークとの構造の違いを中心に説明します。
MEMO 2016年度版と2017年度版のネイチャー論文について
グーグル・ディープマインドのメンバーは、2017年10月に、アルファ碁ゼロの仕組みを解説した下記の新しい論文をネイチャー誌に発表しました。本章は、基本的にこの2017年の論文の解説となります。この論文のことを、以下アルファ碁ゼロ論文と呼びます。
『Mastering the game of Go without human knowledge(人間の知識なしに囲碁を究める)』
(David Silver、Julian Schrittwieser、Karen Simonyan、Ioannis Antonoglou、AjaHuang、Arthur Guez、Thomas Hubert、Lucas Baker、Matthew Lai、Adrian Bolton、Yutian Chen、Timothy Lillicrap、Fan Hui、Laurent Sifre、George van den Driessche、Thore Graepel、Demis Hassabis、 nature、2017)
https://deepmind.com/documents/119/agz_unformatted_nature.pdf
一方、従来版アルファ碁については、2016年1月にネイチャー誌に論文が掲載されています。この2016年の論文のことを、これまで同様アルファ碁論文と呼びます。
『Mastering the game of Go with deep neural networks and tree search(深層ニューラルネットワークと木探索により囲碁を究める)』
(David Silver、Aja Huang、Chris J. Maddison、Arthur Guez、Laurent Sifre、George vanden Driessche、Julian Schrittwieser、Ioannis Antonoglou、Veda Panneershelvam、Marc Lanctot、 Sander Dieleman、Dominik Grewe、John Nham、Nal Kalchbrenner、Ilya Sutskever、Timothy Lillicrap、Madeleine Leach、Koray Kavukcuoglu、ThoreGraepel & Demis Hassabis、nature、2016)
https://storage.googleapis.com/deepmind-media/alphago/AlphaGoNaturePaper.pdf
デュアルネットワークの構造
図1に示すように、デュアルネットワークの入力層から出力層までの構造は、下記のようになっています。
- 入力層:17チャネル
- 第1層:3×3サイズ256種類のフィルタを持つ畳み込み層と、バッチ正規化、ReLU活性化関数
- 第2層~第39層:19個の残差ブロック。なお各残差ブロックは、3×3サイズ256種類のフィルタを持つ畳み込み層、バッチ正規化、ReLU関数各2個からなります。
- 各手の予測確率を計算する次の一手予測部と、勝率を予測する勝率予測部に分岐
-
次の一手予測部の構造:
- 次の一手予測部第1層:1×1サイズの2種類のフィルタを持つ畳み込み層と、バッチ正規化、ReLU関数
- 次の一手予測部第2層:362ノードに出力する全結合層とソフトマックス関数
- 次の一手予測部の出力:362ノード(361個の盤面上の位置と、パスのいずれかを出力する確率に対応)
-
勝率予測部の構造:
- 勝率予測部第1層:1×1サイズ1種類のフィルタを持つ畳み込み層と、バッチ正規化、ReLU関数
- 勝率予測部第2層:256ノードに出力する全結合層とReLU関数
- 勝率予測部第3層:1ノードに出力する全結合層とtanh関数
- 勝率予測部の出力:1ノード(-1.0以上1.0以下の値。+1.0が黒勝ち、-1.0が白勝ちに対応)
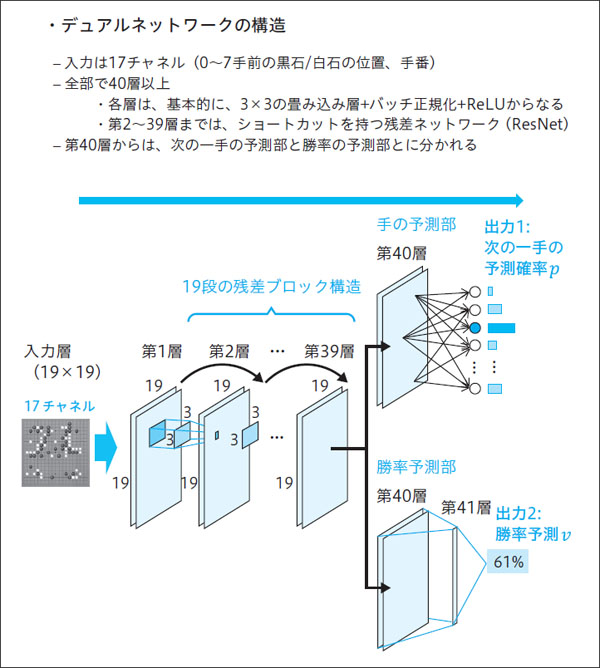
図1:デュアルネットワークの構造。
従来版アルファ碁のポリシーネットワークとバリューネットワークとを統合したような構造となっている
デュアルネットワークの入力に関して
以下、デュアルネットワークの特長的な部分にフォーカスして説明していきます。
最初にデュアルネットワークの入力に関して説明します。従来版アルファ碁では48チャネルあった入力情報(図2(a))が、デュアルネットワークでは石の位置、履歴、手番の計17チャネル(図2(b))となっています。従来版アルファ碁で入力特徴として使われた、空点の位置、連に関する呼吸点の数の情報、シチョウに関する情報などは、使わなくなりました。これらの情報があるほうが、学習は進みやすいと考えられますが、アルファ碁ゼロの「ゲーム固有の情報をなるべく使わない」設計ポリシーにしたがい、使用しなかったと考えられます。
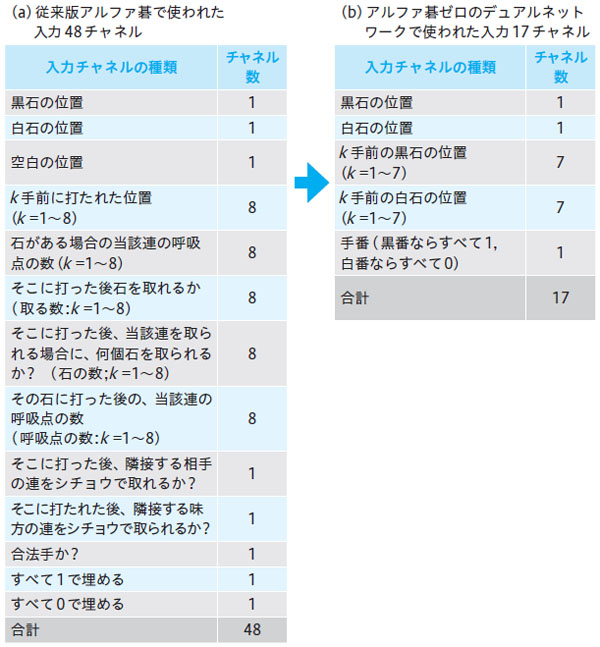
図2:(a)従来版アルファ碁で使われた入力48チャネルと
(b)アルファ碁ゼロのデュアルネットワークの入力17チャネルの内訳。
(b)のほうがかなりシンプルになっている
一方、履歴の入力方法は、従来版アルファ碁(図2(a))では、k(=1~8)手前に打たれた交点そのものだけを入力していましたが、アルファ碁ゼロのデュアルネットワーク(図2(b))では、k(=1~7)手前の黒、白それぞれの石の位置情報をすべて入力しています。これらの情報により、直前に重要となった石の位置を表現することができ、連に関する情報などを補う効果があるのかもしれません。
Column 次の一手予測部の出力にパスが追加されているのはなぜか?
微妙な違いなので見逃してしまいそうですが、次の一手予測部の出力をよく見ると、従来版アルファ碁のポリシーネットワークの出力である(19×19=)361個に「パス」が追加されて出力の個数が362個となっています。実は、このパスは重要な意味を持っています。なぜなら、後述するように、アルファ碁ゼロでは黒番と白番が連続してパスした場合にのみ(厳密に言うと規定の手数を超えてしまった場合も)終局するというルールを採用しているからです。
よって後で説明する強化学習のセルフプレイにおいて、当初のランダムプレイの間は、このパスがたまたま2回続いた時のみ終局することになります。その後、次第に強化学習が進んでくると、自分が勝ちだと思っている場合にのみパスをするようになっていきます。つまりこのパスは、アルファ碁ゼロのルールの環境では、勝ちを宣言するための重要な手となっているわけです。
次の一手予測部と勝率予測部を統合した構造
次に、デュアルネットワークの特長である「次の一手予測部」と「勝率予測部」とを統合した構造について述べます。複数のタスクでモデルの一部を共有し同時に学習する手法のことを、一般にマルチタスク学習(MEMO参照)と呼びます。
アルファ碁ゼロ論文によると、統合した結果として、次の一手予測器としての性能は、ポリシーネットワーク単独の場合よりも落ちるようです。ただし、モンテカルロ木探索に組込んだ場合には、統合したデュアルネットワークのほうが性能は高まるようです。試行錯誤の結果として、総合力としては、デュアルネットワークのほうが優れているとの結論に至ったのかもしれません。
次節で説明するモンテカルロ木探索では、デュアルネットワークの次の一手予測部が出力する手の予測確率pにより探索深さが制御され、勝率予測部が出力する勝率予測vが局面評価関数となります。ゲーム木の探索において重要な、「探索深さ」「局面評価関数」という2要素がここでも登場します。アルファ碁ゼロでは、この重要な2要素が、統合された1つのネットワークモデルにより計算されるわけです。
MEMO マルチタスク学習
複数のタスクの学習に対して、モデルの一部を共有し、同時に学習する手法のことをマルチタスク学習と呼びます。モデルを共有することで、複数のタスクに共通する要因を認識しやすくなり、予測精度の向上が期待できます。デュアルネットワークの場合も、次の一手予測と勝率予測のモデルを一部共有することで、これらの認識に必要となる共通の構造の学習が進みやすくなると考えられます。
残差ネットワーク
最後に残差ネットワーク(ResNet)について少し詳しく説明します。
残差ネットワーク(MEMO参照)は、図3(a)に示した残差ブロックと呼ばれる構造を多段に重ねたものです。デュアルネットワークではこの残差ブロックを19段重ねたものを用いています(図3(b))。
デュアルネットワークの残差ブロックは、この場合、3×3サイズ256種類のフィルタを持つ畳み込み層(3×3 Conv 256)と、バッチ正規化(Bn)、ReLU関数(ReLU)を2回繰り返したものがメイン経路になっていますが、特徴的なのは、このメイン経路を通らないショートカットを持つことです(厳密にいうと図3(a)のように、あるショートカット終了から次のショートカット開始までの間に、ReLUを挟んでいます)。
このショートカットの存在により、実は深いネットワークであっても、浅いネットワークの機能を包含することが知られています。浅いネットワークのみで学習できるようなデータの場合には、浅い段までのパラメータのみが重点的に学習され、残りはショートカット経路を通り、実質的に意味を持たない、というようなイメージです。
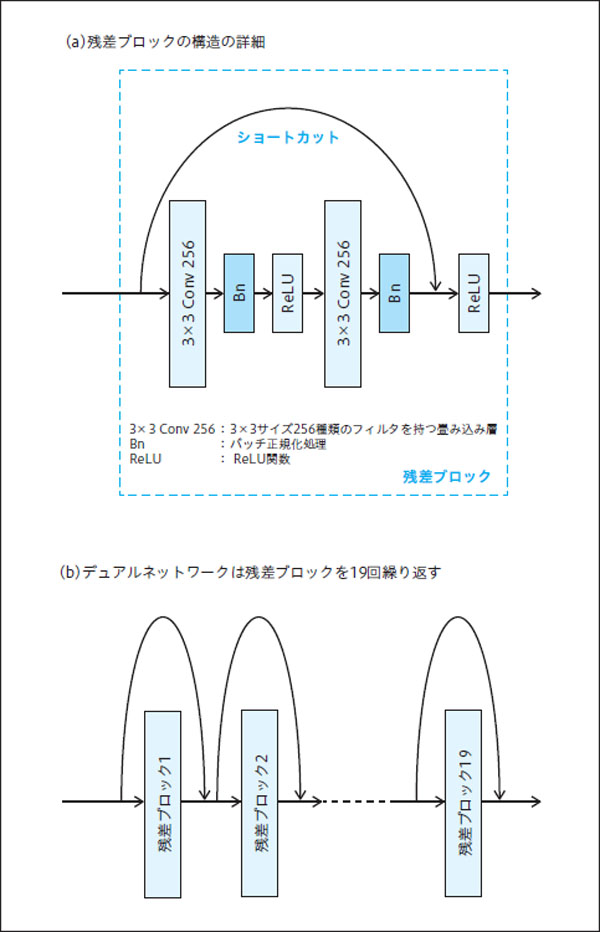
図3:デュアルネットワークの残差ネットワーク部分の詳細。
(a)は残差ブロックの詳細。(b)(a)に示した残差ブロックの構造を19回繰り返している
MEMO 残差ネットワーク
残差ネットワークは2.2.7項で説明したResNetと同じものです。残差ネットワークに関しては、次の論文で説明されています。
『Deep Residual Learning for Image Recognition. Computer Vision and Pattern Recognition(CVPR)』
(Kaiming He、Xiangyu Zhang、Shaoqing Ren、Jian Sun、2016)
https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf
デュアルネットワークの規模と計算量
従来版アルファ碁のポリシーネットワークの場合と同様に、デュアルネットワークの畳み込み層の足し算の回数とパラメータの個数を計算してみましょう。簡単にするため、ここではデュアルネットワークを3×3サイズの畳み込み層が39層あるとみなして計算します。この仮定のもとでは、
-
畳み込みの足し算回数:
19×19×3×3×256×256×(層の数:39)=約83億回 -
フィルタ重みパラメータの個数:
3×3×256×256×(層の数:39)=約2300万個
となります。足し算回数とパラメータ個数が共に、従来版アルファ碁で使われたフィルタ192枚のSLポリシーネットワークの計算量の約6倍となっています。
デュアルネットワークの学習
ここではデュアルネットワークのパラメータ(θとします)の教師付き学習手法について説明します。デュアルネットワークの教師付き学習は、ポリシーネットワークの教師つき学習と基本的に同じであり、誤差関数Lθの勾配を利用する誤差逆伝搬法により、式1のようにパラメータを更新します。αは学習率です。

ただし、デュアルネットワークは手αが出力である確率p(s,a)と黒の勝率v(s)という2つの出力があるため、誤差関数Lθの計算方法がポリシーネットワークとは異なります。
デュアルネットワークに対する正解データは、(π,z)の組からなります。ここで1つ目の正解データπは、ある局面sにおいて各手αが正解となる確率を表します。これはポリシーネットワークの正解データと同様に、強いプレイヤが打った手を正解とする場合は、強いプレイヤの手α*のみを100%とし、残りの手の確率は0%と考えます。後の強化学習の際にはもう少し洗練された確率分布を用います。
次に2つ目の正解データzは、ある局面に対する最終的な勝ち負け(黒勝ちならば+1、白勝ちならば-1)を表します。これは、バリューネットワークの正解データと同じで、この局面から強いプレイヤ同士が打った場合の、最終的な勝敗と思えば良いでしょう。
この条件の下で、重みパラメータをθとするデュアルネットワークfθ(s)の出力の組(p,v)を正解データの組(π,z)に近づける、つまり(p,v)と(π,z)との誤差を最小化するようにパラメータを更新するという方針です。詳細はAppendix 1のA1.1.3項で説明します。
デュアルネットワークの学習の効果
アルファ碁ゼロ論文では、以上で説明したデュアルネットワークを従来版アルファ碁同様に3000万局面を使って教師付き学習した場合、強いプレイヤの手との一致率は60.4%となることが示されています。これは、最高57.0%であった従来版アルファ碁の一致率よりも高い値となっています。残差ブロックを導入し、かつネットワークの深さを深くした効果と言えるでしょう。実際には、教師付き学習ではなく強化学習を使って、デュアルネットワークのパラメータを学習していくわけですが、その手法については別項で述べることにします。
デュアルネットワークの学習部を書く
図4に、従来版アルファ碁のポリシーネットワークの場合と同様に、デュアルネットワークをChainerで記述した場合のネットワーク定義部の例を示します。Chainerを使えば、これまで説明したデュアルネットワークの構造を、比較的簡潔に記述できます。細かい説明は省略しますが、ポリシーネットワークの場合と同様に(a)の部分に、畳み込み、バッチ正規化、全結合等の処理を定義しておき、(b)の部分でこれらの材料を組み立てていきます。

図4:デュアルネットワークをChainerで記述した場合のネットワーク定義部。
従来版アルファ碁のポリシーネットのコードと比較すると、残差ブロックが使われている点、
出力が枝分かれしている点が大きな違いとなる
アルファ碁ゼロのディープラーニングのまとめ
本節で説明した通り、ディープラーニングは、人間の直観を代替する機能を持つと言えるでしょう。囲碁の場合、局面評価関数作成のための特徴量設計がとても難しかったのですが、アルファ碁ゼロは、ついに石の配置と履歴の情報だけから、局面評価する方法を生み出しました。人間の大局観に相当する、囲碁の局面評価関数を作り上げるという、従来不可能と思われていた課題は、ディープラーニングにより見事に解決されたのです。
続きは本書で
本書では、このほかにもアルファ碁からアルファ碁ゼロに至る技術について詳しく解説しています。興味を持った方はぜひ手に取ってみてください。




