はじめに
「技術者のための」と冠した数学書の第2弾がいよいよ完成しました! 本書は、先に出版された『技術者のための基礎解析学』、そしてこの後に続く、『技術者のための確率統計学』との姉妹編になっており、これら3冊で基礎解析学、線形代数学、そして、確率統計学の3つの分野を学ぶことができます。「機械学習に必要な数学をもう一度しっかりと勉強したい」、そんな読者の声が本シリーズを執筆するきっかけでしたが、あらためて振り返ると、「基礎解析学・線形代数学・確率統計学」は、機械学習に深く関連する分野であると同時に、理工系の大学1、2年生が学ぶ数学の基礎、言うなれば、大学レベルの本格的な数学への入り口ともなる領域です。
今、IT業界を中心とするエンジニアの方々からは、機械学習の理解という目的に限らず、もう一度、数学を学び直したいという声を耳にすることが増えてきました。そして、その要望に応じて、大学の教科書とは異なる趣の数学書も増えているようです。そのような中でも、大学生の頃に勉強した、あるいは、さまざまな理由で「勉強しきれなかった」数学をもう一度振り返り、じっくりと腰を落ち着けて勉強し直したいという読者の方には、本シリーズの内容がうまくはまるかもしれません。
線形代数学がテーマの本書では、実数ベクトルに限定して、「一次変換」「行列式」「固有値問題(行列の対角化)」といった定番の内容、そして、ベクトル空間の公理にもとづいた、より一般的なベクトル空間の性質を取り扱います。
線形代数学というと、行列式の性質や対称行列の対角化など、「結果は知っているけれど、なぜそれが成り立つかはわからない」という内容も多いかもしれません。本書では、定義にもとづいた厳密な議論とともに、できるだけ丁寧に計算を進めることで、それぞれの内容について、「確かにその通り」と納得できる説明を心がけました。お好みのノートと筆記具を用意して、本書の説明と、数式にもとづいた議論の展開をみなさんの「手と頭」で、ぜひ再現してみてください。そして、直感的な理解にとどまらない、「厳密な数学」の世界をあらためて振り返り、じっくりと味わっていただければ幸いです。あるいはまた、受験勉強から解放されて、あこがれの大学数学の教科書を開いたあのときの興奮をわずかなりとも思い出していただければ、筆者にとってこの上ない喜びです。
本書について
対象読者
大学1、2年の頃に学んだ数学をもう一度、基礎から勉強したいエンジニアの方
※理系の高校数学の知識が前提となります。理工系の大学1、2年生が新規に学ぶ教科書としても利用いただけます。
本書の読み方
本書は、第1章から順に読み進めることで、線形代数学の基礎を順序立てて学んでいただける構成となっています。数学の教科書では、「定義」「補題」「定理」「系」といった形で、体系立てて主張をまとめる構成も見られますが、本書では、あえてそのような構成にはしていません。1つのストーリーとして本文を読み進めることで、自然な流れの中で、各種の主張が説明・証明されていきます。まずは、お気に入りのノートと筆記具を用意して、本文の説明に従って、丁寧に式変形を追いかけてみてください。本文の中で証明した各種の定理は、各章の最後に「主要な定理のまとめ」としてまとめてあります。本文中では、章末のまとめに対応する箇所を【定理1】のように示してあります。
また、各章の最後には、いくつかの練習問題を用意しました。具体例を通して理解を深めるための計算問題も含めてあるため、本文中の一般的な理論説明だけでは消化不良と感じる際は、ぜひこれらの問題にも取り組んでください。問題数はそれほど多くないので、より多くの計算問題を通して理解を深めたいという方は、演習問題を集めた書籍を別途活用するとよいでしょう。
ただし、機械学習などの応用理論を理解する上では、計算方法だけではなく、「なぜそれが成り立つのか」という理論的な理解もまた大切です。機械学習の教科書や論文では、具体的な数字を使った計算が現われることはほとんどありません。これらを読みこなすために必要となるのは、あくまで、本書の中で進められる議論と同様の理論的な理解です。そのため、本書で解説している「証明」の中身を紙と鉛筆を使いながら、しっかりと自分の頭で追いかけていくことも重要な演習であることを忘れないでください。
各章の概要
第1章 2次元実数ベクトル空間
線形代数学には、一次変換や行列計算など、その基礎となる概念の多くが、2次元の実数ベクトルで説明できるという特徴があります。ここでは、線形代数学の主要な要素となる、ベクトル空間、一次変換、行列計算と行列式、そして、固有値と固有ベクトルについて、まずは、2次元の実数ベクトルでその全体像を把握します。
第2章 一般次元の実数ベクトル空間
第1章で説明した内容をより次元の高いベクトル空間に一般化して議論します。一次変換によるベクトル空間の次元の変化が、対応する行列のランクで表わされることを理解した上で、さらに、行列計算の応用として、行列の基本変形による「掃き出し法」を用いた連立一次方程式の解法を説明します。
第3章 行列式
行列の性質を読み解く鍵となる「行列式」について、その定義を厳密に示した上で、交代性と多重線形性などの基本的な性質、あるいは、行列を構成する列ベクトルの一次独立性との関係などを説明します。さらにまた、余因子を用いて、系統的に行列式と逆行列を決定する方法を紹介します。
第4章 行列の固有値と対角化
行列の固有値と固有ベクトルを見つけることで、行列を対角行列に変換する手続きを説明します。特に、実数成分の対称行列は、この手法によって必ず対角化できることが保証されており、対称行列を含むさまざまな問題を簡単化するテクニックとなります。具体例の1つとして、2次曲面の標準形と主軸を求める方法を紹介します。
第5章 一般のベクトル空間
ここでは、ベクトル空間の公理的な取り扱いを説明します。これにより、実数ベクトル空間に限定されない一般的なベクトル空間の性質、特に、基底ベクトルの存在に関する定理が導かれます。また、基底ベクトルを用いた成分表示と一次変換の表現行列の考え方、そして、基底ベクトルの変換に伴うこれらの変換法則を説明します。
機械学習に必要な数学
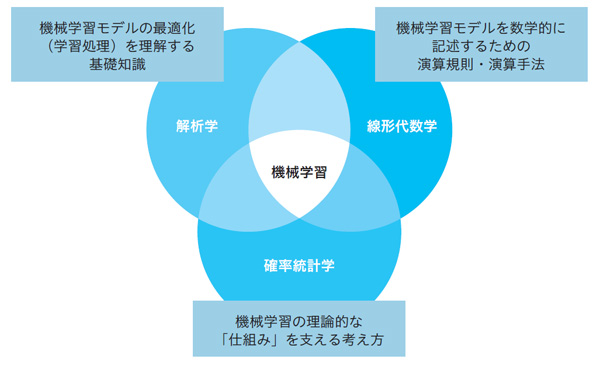
現在、一般に広く活用されている機械学習は、「統計的機械学習」と呼ばれることもあるように、学習用データを通して、現実世界のデータが持つ確率分布を推定するという考え方が基礎になります。そのため、機械学習の理論的な側面を理解する上では、確率分布や条件付き確率など、確率統計学に関する基本的な計算手法に精通する必要があります。
次に、機械学習のモデルを数学的に記述する際は、線形演算がその中心となることが多く、行列を用いた表現が多用されます。また、これに関連して、学習データが持つ特徴量を高次元のベクトル空間の要素として表現することもよく行なわれます。そのため、本書の主題でもある線形代数学で学ぶ行列演算の規則、あるいは、基底ベクトルの線形結合といったベクトル空間上の演算手法にも精通することが求められます。
そして最後に、機械学習の学習処理、すなわち、モデルの最適化では、勾配降下法をはじめとした最適化計算の理解が必要となります。ここでは、解析学(微積分)が重要な基礎知識となります。計算機上で実際に行なう最適化処理としては、勾配降下法が中心となりますが、「何をどのように最適化するべきか」という理論的な導出の過程においては、さまざまな確率分布を含む誤差関数を解析的に調べる必要があります。その意味においては、確率統計学、線形代数学、解析学を組み合わせた総合的な理解こそが、機械学習を支える数学の基礎と言えるでしょう。
続きは本書で
本書ではこのあと線形代数学について、まず直感的な理解を得るところから解説が始まります。最初は線形代数学の役割やベクトル空間の定義を知ることで準備体操し、いよいよ厳密な数学の世界へ足を踏み入れていきましょう。
段階を追って一つずつ解説されていくので、線形代数学をじっくり理解したい方はぜひ本書を手に取ってみてください。




