本書の特徴と使い方
数学が使えるとはどういうことか?
本書の目的は「数学が使えるようになる」ことです。現実の世界で、たとえば集客するとか、不良品を減らすといった問題に対して、数学を適用して解決することです。
それでは「数学が使える」ようになるためには何をすれば良いのでしょうか。「学校で習う問題が解けること」と答える人が多いでしょう。しかし、「学校で習う問題が解けること」と「数学を使えること」は意外なほどに一致しません。
たとえば、x5を微分すると、5x4になります。2x4を微分すると8x3です。つまり、xnを微分するとnxn-1になります。では、3x3を微分するとどうなるでしょうか。掛け算さえできれば、小学生でもすぐにルールを覚えてできるようになることでしょう。
しかし、この問題ができたからといって「微分」を理解しているのか、そして使えるのか、というとそうではないことは明らかです。そして、難関大学の入試に出るような難しい問題でさえも、それが解けることと本当に数学を理解していることが一致しない場合が多いです。
一方、現実の問題を解くときにはコンピュータが使えます。学校のテストで重要な計算の速さや正確さは、ここでは重要ではありません。
数学を実用するときに大事なのは、理論よりもそれがどのような場面で使われるのかという感覚です。残念ながら、これは今の教育課程ではほとんど教えられることはありません。
本書では「Business」という欄を設け、その項目がどのような場面で使われているのかを説明しました。数学を使う感覚を磨くのに役立ってくれると思います。
細かいところに入りすぎない
現在の数学の問題点はあまりにも細かいところに重点を置きすぎることです。もちろん数学という学問は細部が命ではあります。しかし、細部にこだわりすぎて、全体像を見ることがおろそかになっていることは問題です。
本書では、章の最初にIntroduction をはさみ、その章で学ぶ項目の重要性や他の項目とのつながりを示すようにしました。本文中の説明も細かなルールより、全体像がつかめるように配慮しています。
一方、表現はわかりやすさを重視し、省略している部分もあります。説明が厳密でない部分もあるでしょうが、読者のわかりやすさを重視したものですので、ご容赦いただければと思います。
高校数学は結構すごい
本書は高校数学を中心としています。実は高校数学はとても高度です。高校で習う関数や微積分、ベクトルなどを完全に理解していれば、数学を使うために必要な基礎知識はほぼ十分といって良いでしょう。
もちろん、統計や数値解析、線形代数など高校で教えられないけれど重要な項目もあります(本書ではそんな項目もある程度カバーしています)。しかし、高校数学をしっかり理解していれば、それらは難なく理解できるはずです。もし苦戦するのであれば、むしろ高校数学の理解が不十分ではないかと疑ったほうが良いと思います。
また多くの人にとって、数学と一番向き合った時期は入試のときでしょう。本書は受験生をターゲットとしたものではありませんが、受験数学と実用数学の観点を対比させることにより理解が深まると考え、あえて受験生から見た視点も盛り込みました。
特に、受験数学では重要だけど実用数学では重要でない項目、もしくはその逆の項目に注目してみると面白いかもしれません。
本書の使い方
本書の使い方を下に示します。星や概略を参考に、まずは細部でなく、概要をざっくり把握することを優先してください。
知りたい項目だけを辞書的に調べる使い方でも良いですが、できれば一度通読してもらえると、数学の全体像がつかめて良いと思います。

本書では重要性を「教養」「実用」「受験」とターゲット別に分けて示しています。ターゲットと★の数の意味を下に示します。
「教養」の想定ターゲット
メーカー勤務の管理職。文系で数学は高校止まり。技術のマーケティング職について、技術者と会話する最低限の数学力がほしいという人
★★★★★ → 重要な項目です。計算方法も知っておいてください。
★★★★ → 重要な項目です。可能であれば計算もできると良いです。
★★★ → 計算は不必要ですが。言葉の意味は理解してください。
★★ → 余裕があれば言葉の意味を押さえておきましょう。
★ → 教養のレベルでは不必要な知識です。
「実用」の想定ターゲット
電気、情報、機械、建築、化学、生物、薬品などの企業で開発や設計、製造工程の管理などに従事しているエンジニア、プログラマー
データの解析を行うエンジニアやコンサルタントなど
★★★★★ → 仕事で日常的に使います。わからないと恥をかきます。
★★★★ → 仕事でよく使います。計算できるようにしましょう。
★★★ → 仕事で出てくることもあるので勉強しておきましょう。
★★ → 仕事でこれを使うことはあまり多くありません。
★ → 仕事でこの知識が求められることはないでしょう。
「受験」の想定ターゲット
2次試験に数学がある理系の国立大学を受験する高校生
★★★★★ → 基礎の基礎です。考えなくても手が動くようにしましょう。
★★★★ → 頻出です。これがわかっていないと厳しいでしょう。
★★ → 試験に出ます。ちゃんと勉強しましょう。
★★ → 高校数学の範囲内ですが、試験にはあまり出ません。
★ → 高校数学の範囲外です。
下記に、本書から例として対数グラフと物理単位について紹介します。
対数グラフの使い方
数学のテストには出ませんが、世の中でよく使われているので、ぜひマスターしておきましょう。特にエンジニアには必須の知識です。
教養 ★★★★★
実用 ★★★★★
受験 ★
対数軸は等倍したときの長さが同じになる
対数グラフとは対数軸を持つグラフ、変化の範囲が大きい数値をグラフ化するときに使われます。
対数軸の特徴
通常の軸(右図の横軸)は0, 2, 4, 6と差が等間隔ですが、対数軸(同縦軸)は等倍(2→4, 4→8)が等間隔になっています。よって、1, 2, 3, 4, ……と目盛りを振ると右図のようにゆがみます。右図x軸が普通の軸でy軸が対数軸ですが、その逆も、両方対数の場合もあります。軸の片方が対数軸のグラフを片対数グラフ、両軸が対数軸のグラフは両対数グラフと呼びます。

奇妙な軸の意味
対数グラフ(対数軸)は、指数関数のように、桁が変わるほど変化が大きい量の変化を表すときに役立ちます。非常に便利で、世の中でもよく見かけますが、その奇妙な目盛りの打ち方に戸惑う人も多いようです。
これは一見おかしく見えますが、ちゃんとした意味があります。実は普通の軸が同じ差が(つまり、2と4、4と6などが)等間隔になっているのに対し、対数軸では等倍したときの距離が同じになっているのです。
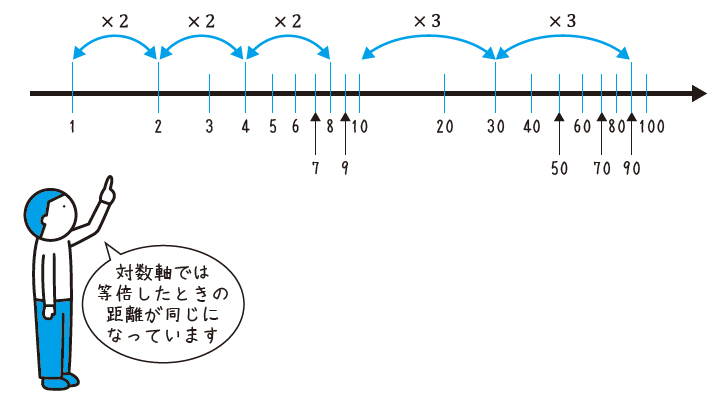
上図で、定規を当てて確認してみると、たとえば1から2、2から4、4から8の距離が同じであることがわかるでしょう。他には1から3と3から9の距離も同じです。もちろん1と10、10と100の距離も同じです。
【Business】ダイオードの電流―電圧特性を対数グラフで表す
下図はダイオードという半導体素子の電流―電圧特性を普通軸と対数軸でグラフにしたものです。普通軸だと0.2~0.6Vは0に張りついていて、変化の様子がまったくわかりません。一方、同じデータでも、対数軸だと関係が正しくつかめることがわかります。
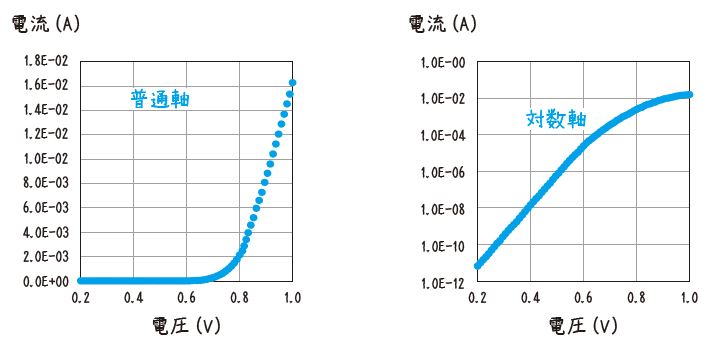
このように対数グラフは便利なものです。しかし、同じデータの見栄えがあまりに変わるため、変化をごまかすテクニックとして使う人もいます。だから、グラフの軸には十分注意しましょう。
指数・対数の物理単位
テストの題材とはなりませんが、よく見かけるので慣れておきましょう。エンジニアにとっては必須の知識です。
教養 ★★★★
実用 ★★★★★
受験 ★
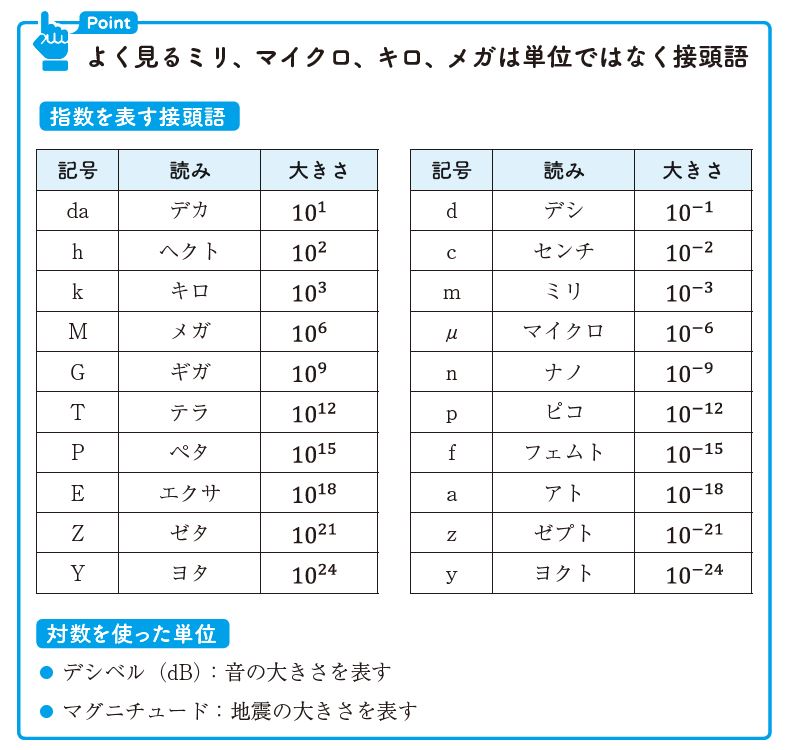
指数を表す接頭語
たとえば1km は1,000m であることはご存じでしょう。ここでk(キロ)というのは1000を表す接頭語です。
大きい数を表す接頭語はコンピュータのデータ量でよく見かけます。コンピュータの世界では、厳密には1,000倍ずつではなく 倍ごとになっています。
小さい数を表す接頭語は、小さい長さを表現するときに1mm(ミリメートル)の1/1000である1μm(マイクロメートル)という単位がよく使われます。普通の人だとこのくらいまで覚えておけば良いでしょうが、物理や電子工学の分野ではf(フェムト)くらいまで日常的に使います。
【Business】デシベルとマグニチュード
対数を使った単位が、世の中にはたくさんあります。たとえば音の大きさを表すdB(デシベル)は、エネルギーが10倍になると10増える量です。つまり20dBは10dB の10倍のエネルギーで30dBは10dBの100倍のエネルギーということになります。
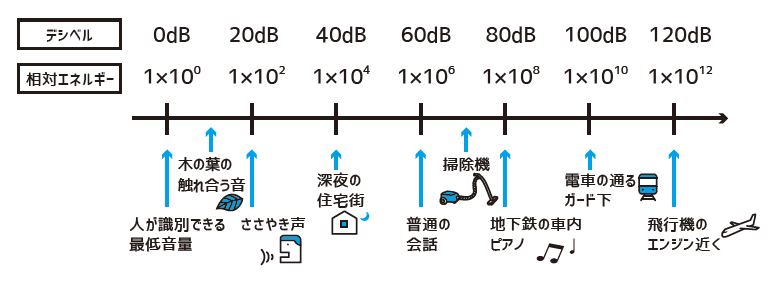
他に身近なところでは地震の単位であるマグニチュードも対数の量です。マグニチュードは2増えるとエネルギーが1,000倍になります。つまり、M(マグニチュード)7の地震は、M5の1,000倍のエネルギーの地震ということです。
2011年の東日本大震災のときに、地震の規模が後にM8.8からM9.0に訂正されました。微細な差に思えますが、この0.2の差はエネルギーがおよそ倍になったことに相当します。対数の単位の増分は感覚以上の差があるのです。
本書ではベクトルや確率・統計も
本書ではこのほか、微積分や数列、ベクトル、複素数、確率・統計といった分野についても紹介。様々な場所で登場する数学の基礎を押さえておくために、本書で効率よく学び直しましょう。




