Pythonで実践する線形探索と選択ソート『Pythonではじめるアルゴリズム入門』より

　プログラミング言語のトレンドは時代とともに移り変わっても、その考え方や利用されるアルゴリズムは変わりません。ソフトウェア開発においてアルゴリズムは効率化や高速化といった恩恵をもたらすため、できれば基本から押さえておきたいところ。今回は、ユーザーの多いPythonでアルゴリズムを学べる『Pythonではじめるアルゴリズム入門』（翔泳社）から、線形探索と選択ソートの手法を紹介します。

本記事は『Pythonではじめるアルゴリズム入門伝統的なアルゴリズムで学ぶ定石と計算量』から一部を抜粋したものです。掲載にあたり編集しています。

線形探索

リストから目的の値を見つけられるようになる。
データ量が多い場合の問題点を体験する。

　多くのデータの中から欲しいデータを見つけることを「探索」といいます。私たちの生活の中でも、欲しいものを見つけるために探す場面はよくあります。そして、その探し方は探すものや量によって変わってきます。

　実際にどのような探索方法があるのか知っておきましょう。

日常生活における探索を知る

　探索を行なうのはプログラミングに限った話ではありません。まず、日常生活における探索について考えてみましょう。

　財布の中に入っている小銭の中から100円玉を探すときを思い浮かべてみてください。人間は色を認識できるため、銀色の硬貨を探します。しかし、銀色の硬貨は他にも50円玉や500円玉もあります。多くの人は財布の中にそれほど多くの硬貨が入っていないので、1枚ずつ順に見てもすぐに見つかるでしょう。

　辞書や電話帳の中から特定のキーワードを探す場合を考えてみると、五十音順に並んだ中から、開いたページより前か後ろかで判断しながらページをめくっていくでしょう。

　一方、書店に行って目的の本を見つけるときを考えてみましょう。多くの本の中から色で探すのは大変ですし、1冊ずつ探していては日が暮れてしまいます。タイトルの順番に並んでいるわけでもないので、多くの場合は目的の本のジャンルで棚を最初に探して、その中から絞り込んでいくでしょう。

　このように、どのようなものを探すのかによって私たちが選ぶ方法は異なります。しかし、どの場合でもすべてを並べて順に探していくと、（必要な時間さえ考えなければ）いずれは求めるものを見つけることは可能です。

プログラミングにおける探索とは？

　プログラミングでも探索の考え方は同じで、データをリストに格納していたとき、そのリストの先頭から順にリストの最後まで調べていけば、いつかは欲しいデータが求められます。もしデータが存在しなくても、最後まで調べることで「存在しない」ということがわかります。

　この方法を「線形探索」といいます。順番に調べるだけなので、プログラムの構造が非常にシンプルで実装も簡単ですし、データの数が少ない場合には有効な方法です。

　たとえば、図4.1のようなリストから目的の値「40」を探すプログラムを作成してみましょう。最初に「50」と比較し、一致すれば探索を終了します。異なれば次の数「30」と比較し、一致すれば探索を終了します。この作業を繰り返すと、「40」と比較したときに一致し、探索を終了できます。

　プログラムでこれを処理するために、まずはデータをリストに格納します。

data = [50, 30, 90, 10, 20, 70, 60, 40, 80]

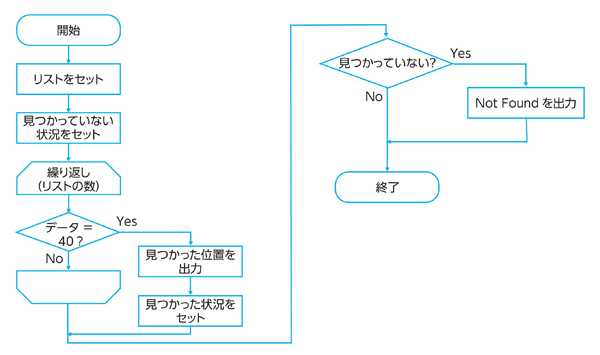
　次に、リストの先頭から順にループしながら、目的の値「40」が見つかるまで探します。見つかった時点でその位置を出力し、処理を終了します。見つからなかった場合は「Not Found」と出力して処理を終了するものとします。

　Pythonでリストの要素を順に処理する場合は、range関数でリストの要素の数だけ繰り返すのが簡単です（リスト4.1）。

リスト4.1　linear_search1.py

data = [50, 30, 90, 10, 20, 70, 60, 40, 80]
found = False ←処理状況を管理する（初期値はFalse）
for i in range(len(data)):
    if data[i] == 40: ←見つけたい値と一致したか？
         print(i)
         found = True ←見つかったことを処理状況としてセット
         break

if not found: ←見つからなかった場合
    print('Not Found ')

　ここではfoundという変数を使って見つかったかどうかを管理しており、見つからなかった場合には「Not Found」を出力しています。また、見つかった場合にはその位置を出力しているだけでなく、breakを使ってループを抜けています。

実行結果　linear_search1.py（リスト4.1）を実行

C:¥>python linear_search1.py
7
C:¥>

線形探索を行なう関数を定義する

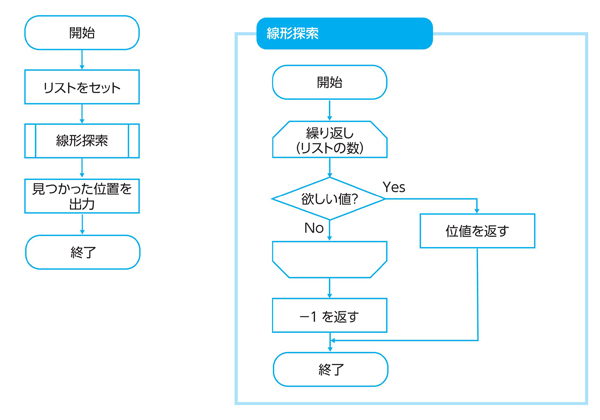
　線形探索は上記のような方法でも十分シンプルですが、実際には関数として定義して使います。見つかったかどうか変数で管理するのではなく、見つかった時点でその位置を返す関数を作成します。

　たとえば、引数として「リスト」と「求める値」を渡してリストでの位置を返す関数を作ります（リスト4.2）。見つかった場合はその位置を、見つからなかった場合は-1を返します。

リスト4.2　linear_search2.py

def linear_search(data, value): ←リストから求める値の位置を検索する関数を定義
    for i in range(len(data)):
        if data[i] == value: ←欲しい値が見つかった場合
            return i
    return -1　　←欲しい値が見つからなかった場合は-1を返す

data = [50, 30, 90, 10, 20, 70, 60, 40, 80]
print(linear_search(data, 40))

実行結果　linear_search2.py（リスト4.2）を実行

C:¥>python linear_search2.py
7
C:¥>

　この方法は順に調べるだけなので理解しやすいアルゴリズムだといえるでしょう。ただし、値が見つかるまですべて調べる必要があるため、データ数が増えると処理に時間がかかります。

　データ数をnとすると、先頭で見つかった場合は1回の比較で終了しますが、最後まで見つからなかった場合はn回の比較が必要です。この場合、比較回数の平均は比較回数の合計をデータ数で割り算して求められるため(1+2+3+…+n)/nとなり、整理すると(n+1)/2回の比較が必要となります（コラム「平均を求める」参照）。最悪の場合はn回の比較が必要なので、O(n)の処理だといえます。

コラム「平均を求める」

選択ソート

選択ソートの処理手順を理解し、実装できるようになる。
選択ソートの計算量を理解する。

小さいものを選ぶ

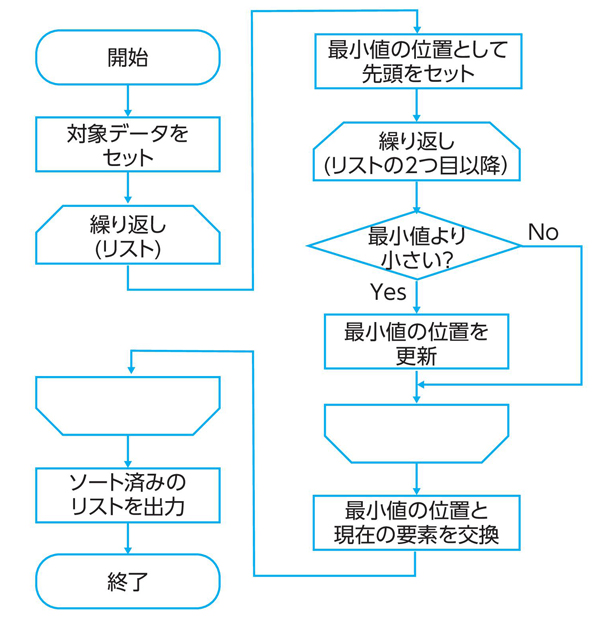
　選択ソートは、リストの中から最も小さい要素を選んで、前に移動する方法です。まず、リストの要素をすべて調べて最小の値を探し、見つかった値をリストの先頭と交換します。

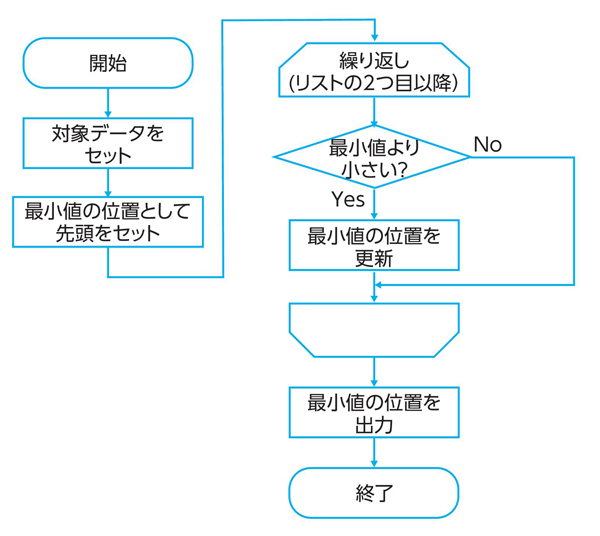
　ここで、リストの中で、最も小さい要素がある位置を見つける方法を考えてみましょう。よく使われる方法として、先頭から順に調べながら、それまでの要素よりも小さい値が登場すれば、その場所を記録する、という方法があります。

　最初に、変数に先頭の位置を入れておき、リストを線形探索のように順に探しながら比べると、リスト5.1のように実装できます。

リスト5.1　search_min.py

data = [6, 15, 4, 2, 8, 5, 11, 9, 7, 13]

min = 0 ←最小値の位置の初期値として先頭を設定
for i in range(1, len(data)):
    if data[min] > data[i]:
        min = i ←最小値が更新されたらその位置をセット

print(min)

　これを実行すると、最小の要素である「2」の位置として「3」が出力されます。

実行結果　search_min.py（リスト5.1）を実行

C:¥>python search_min.py
3
C:¥>

　これを選択ソートでも使います。最初は、リスト全体の中から最小の値を探し、見つかった位置（の値）と先頭（の値）を交換します（図5.2）。

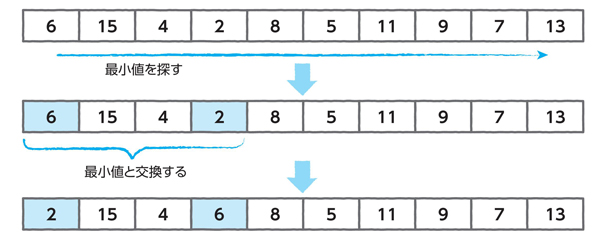
　次に、リストの2 番目以降の要素から最小の値を探し、2番目（の値）と交換します。これをリストの最後の要素まで繰り返すと、ソートが完了です。

選択ソートの実装

　Pythonで実装すると、リスト5.2のように書けます。

リスト5.2　select_sort.py

data = [6, 15, 4, 2, 8, 5, 11, 9, 7, 13]

for i in range(len(data)):
    min = i ←最小値の位置をセット
    for j in range(i + 1, len(data)):
        if data[min] > data[j]:
            min = j ←最小値が更新されたらその位置をセット

    # 最小値の位置と現在の要素を交換
    data[i], data[min] = data[min], data[i]

print(data)

　内側のループは、先ほど紹介した最小の値を探す方法を使っています。調べたものより小さい値が見つかったリストのインデックスを保存しておき、ループを抜けた後にそのインデックスにある値と交換しています。

　このプログラムを実行すると、次の結果が得られ、正しく並べ替えられていることがわかります。

実行結果　select_sort.py（リスト5.2）

C:¥>python select_sort.py
[2, 4, 5, 6, 7, 8, 9, 11, 13, 15]
C:¥>

選択ソートの計算量

　1つ目の最小値を探すには、残りのn‒1個の要素と比較が必要で、同じように2つ目の最小値を探すにはn‒2回の比較が必要です。このため、全体での比較回数は(n‒1)+(n‒2)+…+1=n(n‒1)/2となります（この計算については、第4章のコラム「平均を求める」を参照してください）。

　入力されたデータが小さい順に並んでいた場合、入れ替えは一度も発生しませんが、比較は必要です。比較回数であるn(n‒1)/2はn²/2-n/2と変形できますが、前半のn²と比べて後半のnの部分はnの値が大きくなると無視できるため、その計算量はO(n²)です。

コラム「連結リストでのソート」

　本書では、ソートのアルゴリズムを紹介するときのデータ構造にリスト（配列）を使っています。しかし、実際には連結リストで構成されたデータを使うこともあるでしょう。もちろん、連結リストであってもリストと同じような手法でソートを実装することは可能ですが、単純に要素番号でアクセスするのではなく、各要素が持つ次のアドレスを書き換える必要があります。

　以降で解説するソートについても、読み終えた後に連結リストでのソートを実装してみてください。そして、その計算量についても考えてみてください。ソートの手法について理解が深まるだけでなく、連結リストも使いこなせるようになるので一石二鳥ですよ。

Amazon　SEshop　その他

Pythonではじめるアルゴリズム入門
伝統的なアルゴリズムで学ぶ定石と計算量

著者：増井敏克
発売日：2020年1月24日（金）
価格：2,200円＋税

本書は、初心者にも扱いやすいプログラミング言語「Python」を使用して、アルゴリズムの基礎・考え方を学ぶ入門書です。Pythonがはじめてという方のために、第1章ではPythonの基本とデータ構造について解説しています。

Pythonで実践する線形探索と選択ソート 『Pythonではじめるアルゴリズム入門』より