Pythonでアルゴリズムに入門する！ 押さえておきたい二分探索とバブルソートとは？

二分探索

• 線形探索と比べて処理時間が大幅に短くなることを体感する。
• 事前にソートが必要なことを理解する。

探索範囲を半分に分ける

　データ数が増えても高速に処理する方法を考えると、私たちが辞書や電話帳から探すときに似た方法が考えられます。ある値を見たときに、目的の値がそれよりも前か後ろかを判断する方法です。この方法を使うには、データが五十音順など規則的に並んでいる必要があります。

　ここでは、次のようなリストにデータが昇順で格納されているとします。

data = [10, 20, 30, 40, 50, 60, 70, 80, 90]

　ここから40という値を探してみます（図4.2）。最初に中央の値50と比較すると、40はこれより小さいため、前半を探せばよくなります。次は10、20、30、40の中央にある20と比較します。すると、今度は20よりも大きいため、後半を探します。

　そして次は30と比較し、後半を探します。その後40と比較して一致すると、ここで探索は終了となります。このように、探索範囲を前か後ろの半分に区切って探索することを繰り返します。今回は比較した回数が4回でした。

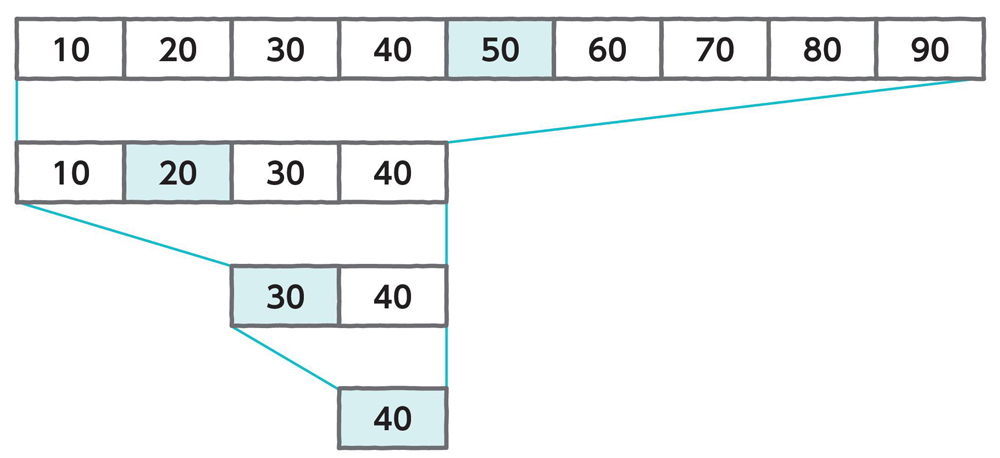
　このように、データが昇順に並んでいる中から、目的のデータが真ん中より右にあるか左にあるかを調べる作業を繰り返します。実際にPythonのプログラムで実装してみましょう（リスト4.3）。リストの左端と右端から、探す位置を半分に絞り込みながら順に探索します。

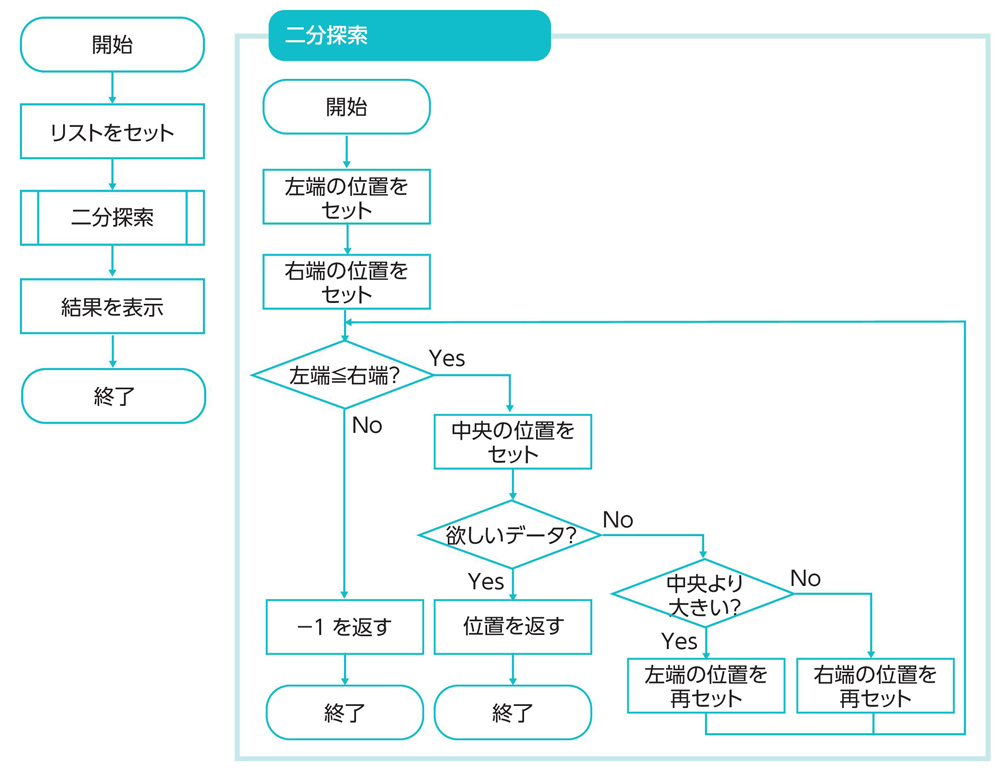
def binary_search(data, value):
    left = 0            # 探索する範囲の左端を設定
    right = len(data) - 1            # 探索する範囲の右端を設定
    while left <= right:
        mid = (left + right) // 2            # 探索する範囲の中央を計算
        if data[mid] == value:
            # 中央の値と一致した場合は位置を返す
            return mid
        elif data[mid] < value:
            # 中央の値より大きい場合は探索範囲の左を変える
            left = mid + 1
        else:
            # 中央の値より小さい場合は探索範囲の右を変える
            right = mid - 1
    return -1            # 見つからなかった場合

data = [10, 20, 30, 40, 50, 60, 70, 80, 90]
print(binary_search(data, 90))

C:\>python binary_search.py
8
C:¥>

　ここでは、leftとrightという2つの変数を使って、範囲を絞り込んでいます。一致したときにはその位置を返し、一致しなかったときにはleftとrightの値を再設定しています。

データが増えたときの比較回数を考える

　一見すると複雑な処理を行なっているように見えますが、図4.2を見ると探索範囲がどんどん絞られていくことがわかります。この効果は、データの数が増えたときの比較回数に現れます。

　一度比較すると探索範囲が半分になる、ということは、リストに含まれるデータ数が2倍になっても最大の比較回数は1回増えるだけです。これは、数学の対数の考え方が使えます。対数は指数の逆の考え方で、たとえばy=2^xからxを求める式はx=log₂yと定義されています。

　指数は第3章でも登場したように、右肩の値が増加すると急激に大きくなります。たとえば、2¹=2、2²=4、2³=8と増えていき、2¹⁰=1,024、2¹⁶=65,536となります。一方の対数はlog₂2=1、log₂4=2、log₂8=3となり、log₂1,024=10、log₂65,536=16のようにlogの中が増えても大きく変わりません。

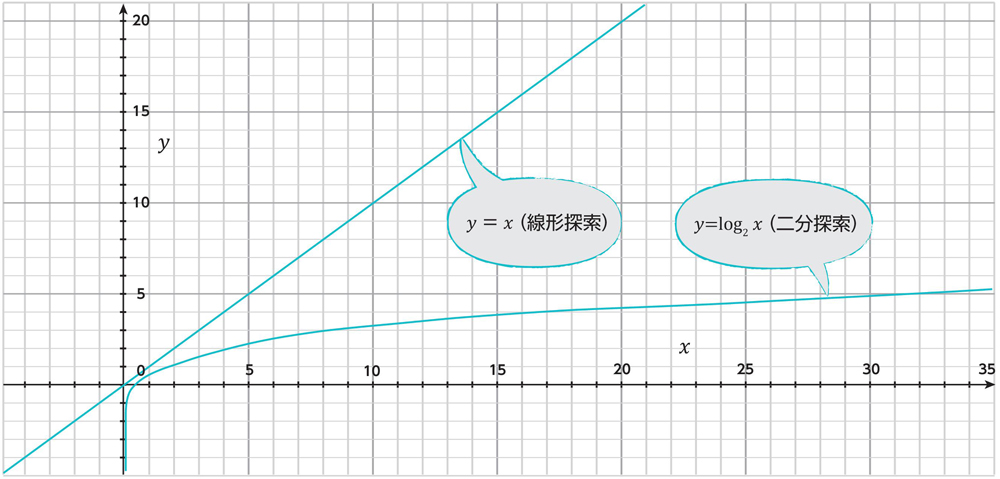
　実際、y=xのグラフとy=log₂xのグラフを描いてみると、図4.3のようになります。y=log₂xはy=2^xのグラフと、y=xで線対称であり、xの値が増えてもyの値はあまり増えないことがわかります。

　二分探索の場合、比較回数の増え方は対数のペースであるため、データ数が1,000個程度に増えても比較回数は10回程度、100万個に増えても比較回数は20回程度です。線形探索だと1,000個になると1,000回、100万個になると100万回かかっていたものと比べると図4.3のように圧倒的な差が生まれることがわかります。

　なお、O(n)やO(n²)で定数倍を無視するのと同じように、対数の底の違いは無視できます。このため、オーダーを書くときは底を省略することが一般的で、二分探索はO(log_n)と表現できます。

　一般的には、線形探索よりも二分探索のほうが高速に処理できますが、データが昇順か降順に並んでいる必要があるため、事前にデータの並べ替えが必要です（線形探索の場合には並び順は関係ない）。また、データの個数が少ない場合には処理速度に大きな差が出ないことから、線形探索が使われることも少なくありません。

　扱うデータの量やデータの更新頻度なども検討した上で、探索方法を決めることが必要です。

Column　スキップリスト

　この節ではリスト（配列）に対する二分探索を紹介しましたが、実際にはソートされた連結リストに対して高速に探索したい場合もあります。しかし、連結リストは前から順にたどる構造のため、単純には二分探索はできません。

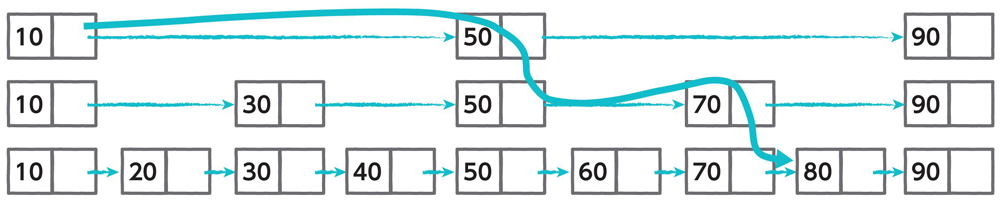
　そこで、連結リストのデータ構造を工夫したものに「スキップリスト」があります。電車で各駅停車以外に急行や特急があるように、順にたどるのではなく、一部を読み飛ばせるデータ構造です（図4.4）。

　スキップリストを使うと、連結リストでも効率よく探索できます。もちろん、挿入や削除なども余分に実装しなければなりませんが、便利なデータ構造として知っておきましょう。

バブルソート

• バブルソートの処理手順を理解し、実装できるようになる。
• バブルソートの計算量を理解する。

隣同士で交換する

　選択ソートも挿入ソートも、リストの要素を交換しながら処理しています。このため、「交換ソート」と呼べなくもありませんが、一般的に「交換ソート」というときは「バブルソート」のことを指します。

　バブルソートは、リストの隣り合ったデータを比較して、大小の順序が違っているときは並べ替えていく方法です（図5.5）。データが移動していく様子を、水中で泡が浮かんでいく様子に例えて、バブルソートという名前が付けられています。

　リストの先頭と次のデータからはじめて、左のほうが大きければ右と交換することを、1つずつずらしながら繰り返します。リストの最後尾まで到達すると、1回目の比較は終了です。

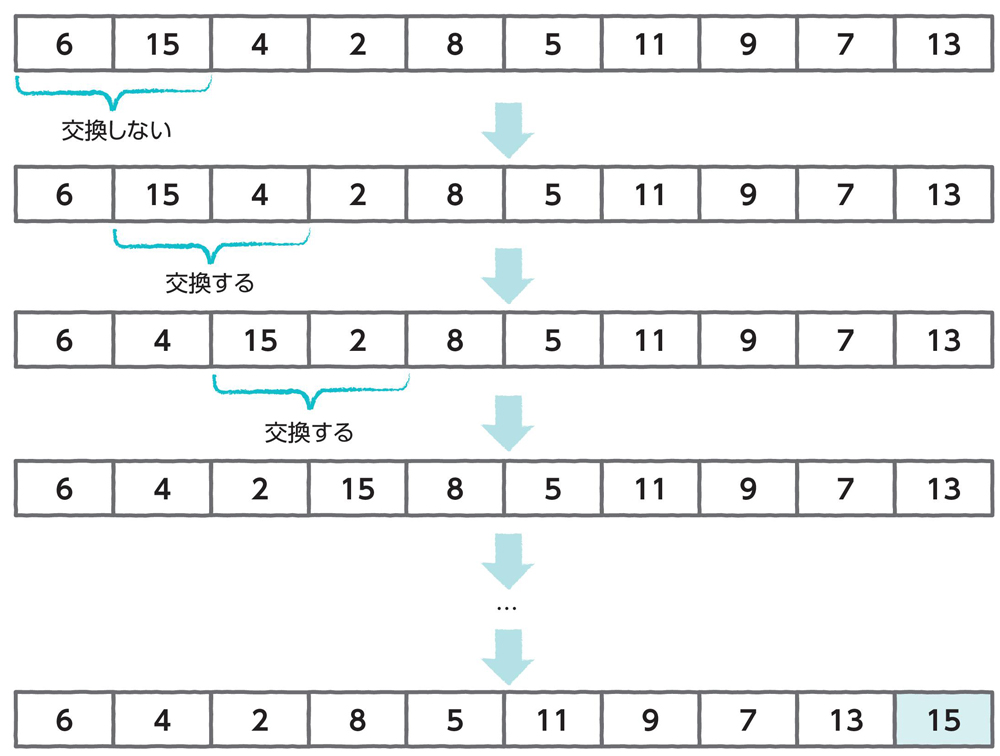
　このとき、リストの最後尾にはデータの最大値が入ります。2回目は一番右端を除いて同様の比較を行なうと、最後から2番目が決まります。これを繰り返すと、すべてが並べ替えられ、ソートは終了です。

バブルソートの実装

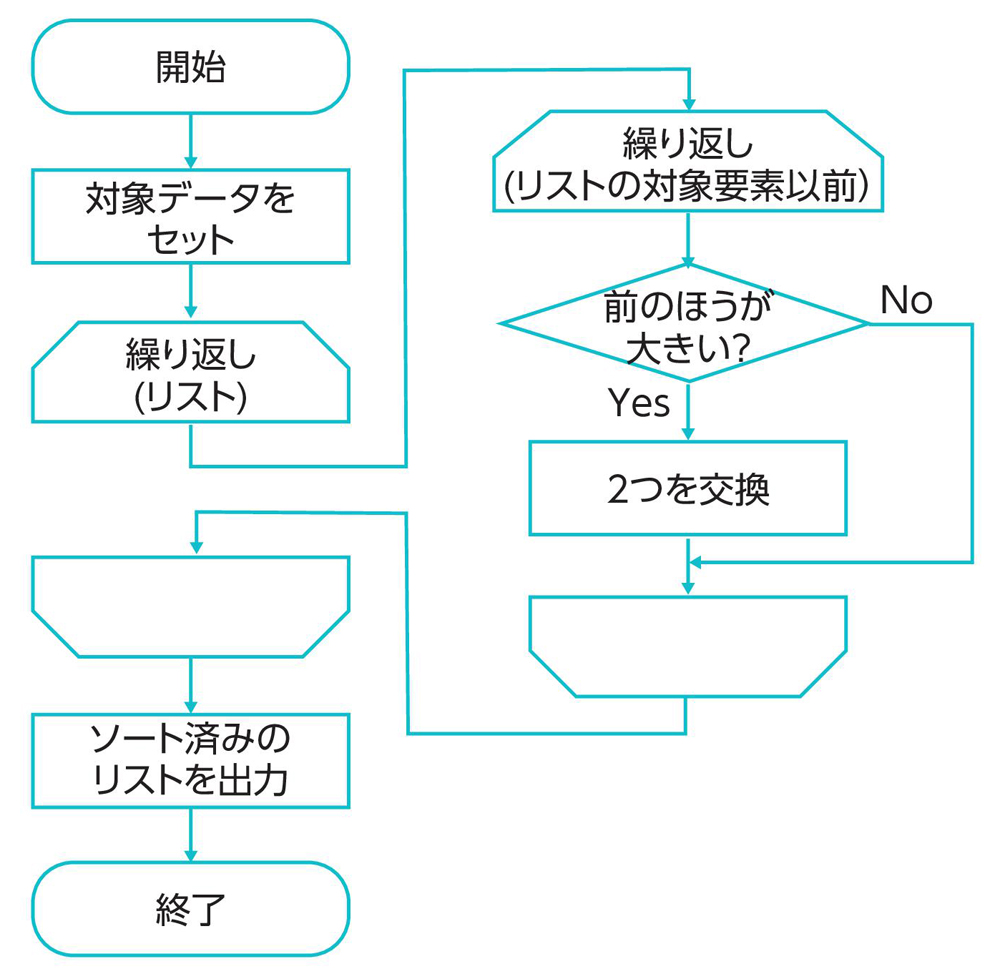
　これをPythonで実装すると、リスト5.4のように書けます。

data = [6, 15, 4, 2, 8, 5, 11, 9, 7, 13]

for i in range(len(data)):
    for j in range(len(data) - i - 1):    # ソート済みの部分以外でループ
        if data[j] > data[j + 1]:    # 前のほうが大きいとき
            data[j], data[j + 1] = data[j + 1], data[j]

print(data)

C:¥>python bubble_sort.py
[2, 4, 5, 6, 7, 8, 9, 11, 13, 15]
C:¥>

　バブルソートは、1回目にn‒1回の比較・交換を行ないます。また、2回目には、n‒2回の比較・交換を行ないます。このため、比較・交換の回数は、(n‒1)+(n‒2)+…+1=n(n‒1)/2と計算できます（これは選択ソート、挿入ソートと同様）。

　この回数は、入力データがどのような並び順であっても同じです。入力されたデータが事前に並んでいると交換は発生しませんが、比較は同じだけの回数を行なわなければなりません。つまり、上記のように実装すると、計算時間はデータの並び順にかかわらず常にO(n²)です。

バブルソートの改良

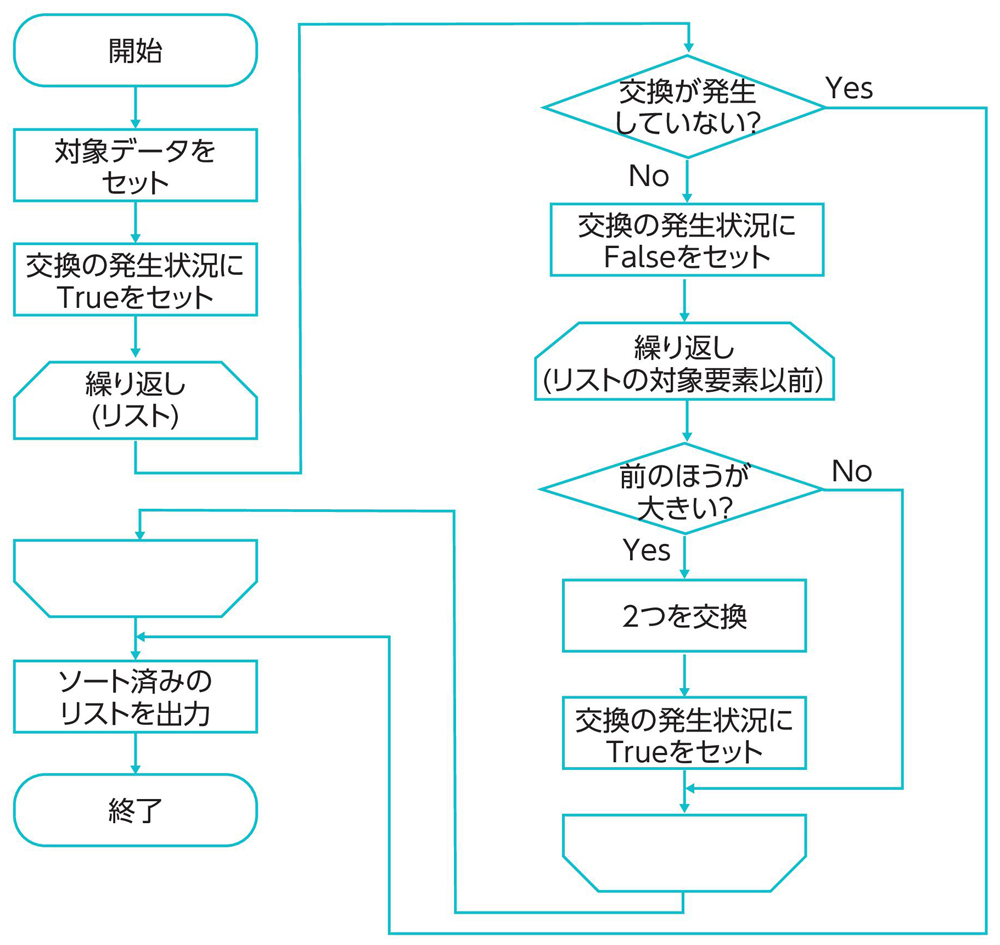
　バブルソートで変更が発生しなかった場合に処理を打ち切り、高速化することを考えます。処理中に交換が起こったかどうかを記録し、交換が起こらなかった場合はそれ以降の処理を行なわないものとします。

　たとえば、リスト5.5では、交換が発生したかどうかを保存するchangeという変数を用意しています。交換が発生しているとchangeにTrueという値を、発生していない場合はFalseという値をセットしています。そして、交換が発生しなかった場合は、ループを抜けて処理を終了しています。

data = [6, 15, 4, 2, 8, 5, 11, 9, 7, 13]

change = True
for i in range(len(data)):
    if not change:    # 交換が発生していなければ終了
        break
    change = False    # 交換が発生していないものとする
    for j in range(len(data) - i - 1):
        if data[j] > data[j + 1]:
            data[j], data[j + 1] = data[j + 1], data[j]
            change = True    # 交換が発生した

print(data)

　このように改良すると、ソート済みのデータが与えられた場合は外側のループを一度だけ処理して終了するため、計算時間がO(n)となります。ただし、一般的にはソート済みのデータが与えられることは少なく、最悪時間計算量がO(n²)であることは変わりません。

Amazon　SEshop　その他

Pythonではじめるアルゴリズム入門
伝統的なアルゴリズムで学ぶ定石と計算量

著者：増井敏克
発売日：2020年1月24日（金）
価格：2,200円＋税

本書について

本書は、初心者にも扱いやすいプログラミング言語「Python」を使用して、アルゴリズムの基礎・考え方を学ぶ入門書です。特にPythonがはじめてという方のために、第1章ではPythonの基本とデータ構造について解説しています。