ロジスティック回帰分析・プロビット回帰分析

年収と持ち家の関係性を回帰分析する
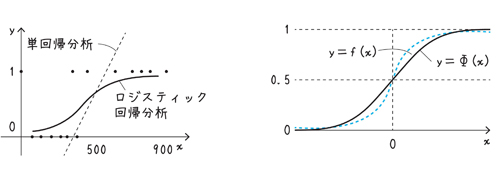
年収と持ち家の関係を調べるアンケートを取りました。年収をx、持ち家の人をy=1、持ち家でない人をy=0としてデータを取ったところ、上左図のような散布図になりました。xとyで単回帰分析をすると、回帰直線では負の値や1以上の値が出てきてうまくありません。そこで、直線の代わりに、xが大きくなるに従って1に近づき、xが小さくなるに従って0に近づくような関数を用いて回帰分析をしようというのが、ロジスティック回帰分析やプロビット回帰分析です。
x→∞で1、x→-∞で0となるような関数として、f(x)やF(x)が選ばれたわけです。y=f(x)、y=F(x)のグラフは前ページの右図のようになります。
前ページの左図実線のようなグラフを得ることができれば、yの値は年収xの人が持ち家である確率を表していると解釈できます。この例の他、毒物の摂取量と致死率、温度と発芽率などにも適用できます。
得られたデータ(xi,yi)から、a、bを求めるには最尤法(05章03節)を用います。すなわち、プロビット分析であれば、尤度関数を
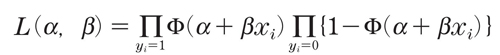
と設定します。線形回帰の場合と異なり、a、bの最尤値は(xi,yi)を用いて明示的に表すことはできません。そこで、コンピュータによる数値計算で求めます。
ロジスティック回帰と対数オッズは関連がある
ロジスティック回帰の式で
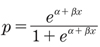
と置くと、
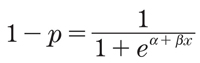
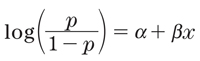
となります。確率pに対して、p/(1-p)をオッズ(odds)、log[p/(1-p)]を対数オッズまたはpのロジット関数といいます。ロジスティック回帰分析とは、対数オッズをxの1次式で表すモデルを用いた回帰分析であるといえます。
説明変数をk個にして、

をモデルにした場合も同様に、ロジスティック回帰分析、プロビット回帰分析といいます。
なお、(x1,x2,……,xk,y)(yは0または1)型の予測は判別分析でもできます。しかし、この回帰分析のように予測値が0から1までの実数値で返ってくるわけではありません。
分散分析(概説)

変動(平方和)から分散比を作る
分散分析はフィッシャーがロザムステッド農事試験場に勤めているとき、農作物に適した生育条件(肥料、日照、気温、土壌など)を研究するために開発した統計手法です。異なる条件のもとでの収穫量を比較し、効果に差があるか否かを検定するのです。
A1、A2、A3の3つのグループがあり、それぞれの平均をm1、m2、m3とします。A1、A2、A3から抽出した標本から、帰無仮説H0:m1=m2=m3を検定するのが分散分析の基本形です。2群の差の検定を繰り返すことでm1、m2、m3に差があるかを検定してはいけない理由についてはIntroductionで述べたので繰り返しません。
帰無仮説を検定するために、分散分析では検定統計量として分散比を作ります。標本全体での偏差平方和STを分散分析では全変動(total variation)または全平方和(SST:sum of squares total)と呼びます。分散比を作るために、これをいくつかの変動の和に分けます。
たとえば、03節の二元配置分散分析(繰り返しなし)では、
(全変動)=(A群間変動)+(B群間変動)+(誤差変動)
といった具合です。各変動には自由度が計算されています。変動を自由度で割って分散にしたあと、組み合わせて分散比を作ります。これが検定統計量になります。分散比をF分布で検定するのが分散分析に共通した手法です。F検定にかけるので分散比のことをF値とも呼びます。
このあらすじを頭に入れて、実例から先に当たるのが良いでしょう。統計学の利用だけを目指している方は、次の分散分析表の読み方さえできれば十分です。
分散分析は各グループ内の分散が互いに等しいことを仮定しています。この前提条件が成り立たない場合は分散分析ができないので注意しましょう。
二元配置分散分析(繰り返しあり)では、単にグループの平均が等しいかどうかだけでなく、要因どうしの交互作用(相乗効果や相殺効果)があるか否かまで検定できるところが興味深いところです。
自動車のアクセサリーを売り込むのはどこが良いか?
カーアクセサリーの会社を経営するH氏は、世界の6地域(アジア、アフリカ、オセアニア、ヨーロッパ、南アメリカ、北アメリカ)、83か国に関する国民1,000人当たりの自動車保有台数のデータを用いて、自動車の平均保有台数に地域差があるのかを分散分析することにしました。統計ソフトの結果(分散分析表)は次のようになりました。
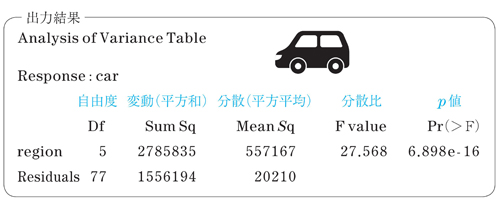
この検定は自由度(5,77)のF分布で検定します。分散比(F value)が27.568で、p値が6.89*10-16ですから、有意水準1%でも帰無仮説は棄却、すなわち自動車の平均保有台数には地域差があることになります。分散分析表を読むポイントは、Pr(>F)の値です。これが有意水準より小さければ帰無仮説を棄却、大きければ帰無仮説を受容します。分散分析は要約するとこれだけです。
共分散構造分析
パス図を設計する
共分散構造分析でははじめにパス図を設定します。いわば分析の設計図です。
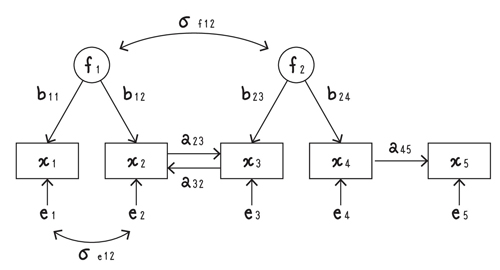
上のパス図を式にすると、
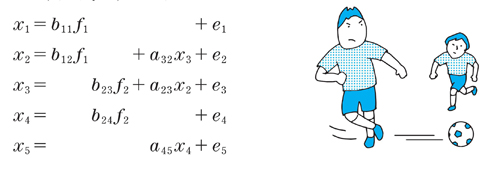
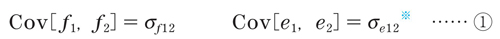
となります。このように、パス図の→は係数を、↔は共分散、相関係数を表しています。
観測できる変数を観測変数(xi)、因子分析で共通因子と呼んでいたものを潜在変数(fi)、独自因子と呼んでいたものを誤差変数(ei)といいます。
観測変数xiを潜在変数fiを用いて表した式(x1からx4まで)を測定方程式、観測変数どうしの関係を表した式(x5)を構造方程式といいます。測定方程式は因子分析、構造方程式は回帰分析をしていると見なせますから、共分散構造分析は「回帰分析と因子分析を合わせた分析方法」であると標語的に表現されます。
f2からx1、x2にパスがなくても良いし、x2とx3に1次の関係があっても良いし、潜在変数どうし、誤差変数どうしに相関関係があっても良い、というように分析者が自由度を持ってモデルを構築できるところが共分散構造分析の利点です。
観測データx=(x1,x2,x3,x4,x5)は、各成分の期待値が0になるように中心化(xiに対してxi-xで置き換える)されているものとします。xから、
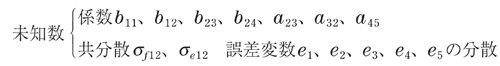
を決めるのが目標です。
共分散構造分析で適材適所に配置しよう
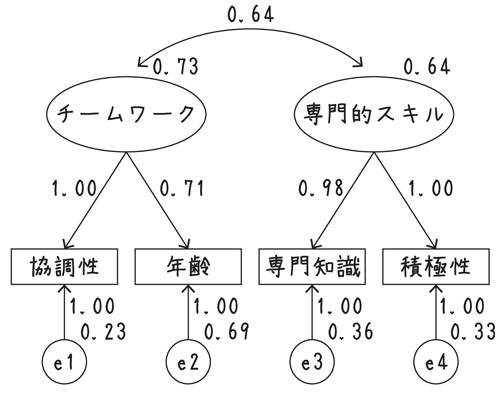
人事部長のF氏は、チームワークと専門的スキルを両方とも生かす組織作りに頭を悩ませていました。ある調査の共分散構造分析の結果を使って、各人の協調性、年齢、専門知識、積極性のアンケートから、チームワークと専門的スキルを割り出し、人材の配置を行った結果、最適な組織を作ることができました。
ギブスサンプリング

ギブスサンプリングのイメージ
Pointのアルゴリズム自体はベイズ統計でなくとも使えるものです。
ベイズ統計ではh(x,y)を事後分布とします。上のアルゴリズムで(x,y)の標本を作ったあと、その標本をもとにモンテカルロ積分を用いてx、yの平均・分散・分布などをベイズ推定します。
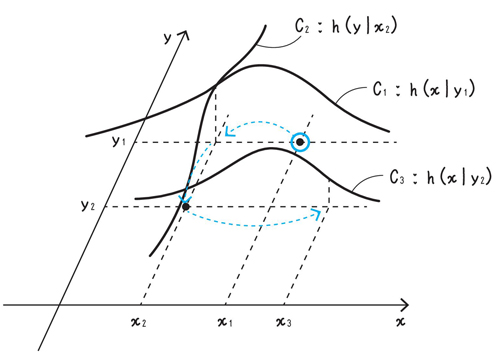
ギブスサンプリングのアルゴリズムをイメージ化すると上の図のようになります。
図の曲線C1は、周辺確率密度関数h(x|y1)のグラフになっています。これを用いて確率的にx2を取ります。次に、曲線C2が表す周辺確率密度関数h(y|x2)を用いてy2を取ります。このようにして順繰りに(x,y)の標本を取り出していくのです。
「h(x|yi)を用いて確率的にxi+1を取る」のですから、yiに対してxi+1が一意に定まるわけではありません。xi+1=1のこともあるかもしれないし、xi+1=2のこともあるかもしれないということです。周辺確率を使ってランダムウォークしているイメージです。
ただ、h(x|yi)を用いて何回もxを取れば、h(x|yi)が大きいところでは高密度で、小さいところでは低密度でxが取られ、h(x,y)の分布に沿った標本を作ることができるわけです。
このようなことはh(x,y)の関数の型によって容易である場合もありますが、困難な場合もあります。「h(x|y)、h(y|x)の標本が容易に作れる」と断っているように、容易な場合に限ってギブス法は有効です。
データが高次元のときにギブスサンプリングが活躍する
図が描けるようにPointでは2次元の場合で説明しましたが、もちろんk次元に拡張可能です。次元が大きいとき(k次元とする)は、k個の乱数を発生させてサンプルを作ろうとすると、計算量が大きくなってしまいます。そこで、効率よく標本を作るために用いるのがギブスサンプリングなのです。
(q1,q2,……,qk)に対して、標本を取りやすい周辺確率密度関数
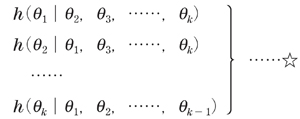
を用いて、順繰りにq1、q2、……、qkの標本を取り出していけば良いのです。
(q1,q2,……,qk)に対して☆の式が与えられているとき、完全条件付き分布が与えられているといいます。完全条件付き分布が与えられているとき、ギブスサンプリングが使えます。




