ベイズの定理の導出
ベイズ統計学において、確率は観察された結果の割合の尺度としてではなく、主観的に事柄(信念)をどの程度信じるかの尺度として扱われます。ベイズ推定の文脈では、データを観測した後にその信念の度合いを更新する規則として、ベイズの定理という規則が使用されます。
ベイズの定理の概要を掴み、条件付き確率P(A|B)とP(B|A)の関係を理解しましょう。AとBの同時確率は以下の2つの式のように、条件付き確率と周辺確率の積で計算できます。
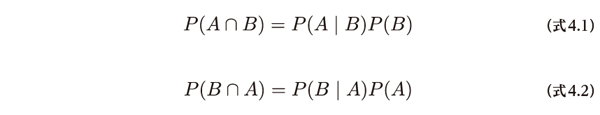
P(A|B)はBが与えられたときのAの条件付き確率を表しています。P(A|B)は必ずしもP(B|A)と同じではありません。AとBの同時確率については次の関係があり、同時確率は(式4.1)と(式4.2)のどちらで計算しても同じ結果になります。
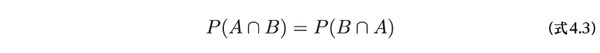
以上の3つの式から次の関係が成り立ちます。
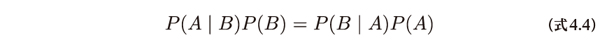
この式の両辺をP(B)で割るとベイズの定理が得られます。
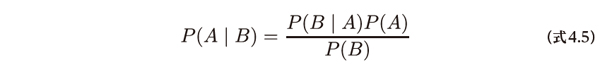
ベイズの定理はP(A)、P(B)、P(A|B)、P(B|A)の間の関係を表しています。ベイズの定理の大切なポイントは、ベイズの定理が条件付き確率を計算する式であり、この章の焦点であるP(A|B)とP(B|A)の関係を説明していることです。つまりベイズの定理はある条件付き確率P(A|B)がわかっているとき、その逆であるP(B|A)を求めるために使用できます。
ベイズの定理の利用例
架空の病気の検査を例として、ベイズの定理の利用方法を説明します。日本国内で、ある病気の患者の割合は0.1%であるとわかっているとします。その病気を発見する検査法は、病気に罹患している人のうち99%の人が陽性反応を示します。また、病気でない健康な人が検査を受けても3%の人が陽性反応を示してしまいます。さて、日本国内に住むDさんがこの検査を受けたら陽性反応が出ました。Dさんが病気に罹患している確率はどのくらいでしょうか。
この例題の事象を以下のように表すとしましょう。また、事象の関係は図4.1となります。
- 事象A:病気である
- 事象A:健康である
- 事象B:検査結果が陽性
- 事象B:検査結果が陰性
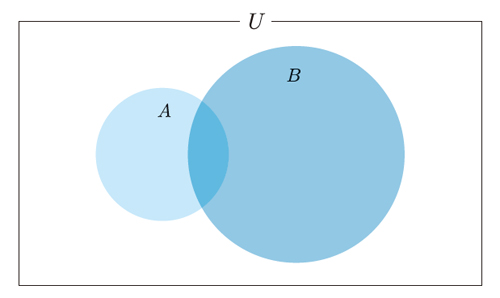
Dさんが検査を受けて陽性反応が出た場合、実際に病気に罹患している確率P(A|B)をベイズの定理を使って求めてみましょう。この例の特殊なところは、架空の設定ではありますが、すでに客観的なデータが得られているとして周辺確率P(A)などが定まっていることです。ベイズの定理の(式4.5)に値を代入していくだけで目的の条件付き確率が求まります。
標本空間は病気の検査を受けているすべての人で構成されています。この人達の中で0.1%がその病気になっているので、逆に99.9%の人は病気ではありません。これらは確率P(A)とP(A)なので次のように書けます。
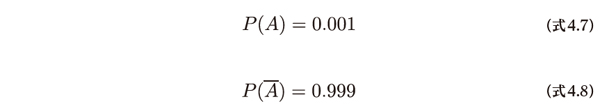
また、病気の患者が検査を受けると陽性の結果となる確率が99%とわかっています。これは条件付き確率であり次式で表されます。
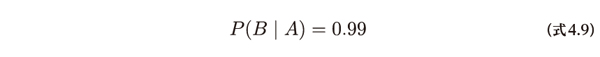
次にベイズの定理を利用するために周辺確率P(B)を求めていきます。まずは病気であり、かつ検査結果が陽性である同時確率P(B∩A)を計算します。(式4.2)を使うことで、次のようにその確率を計算できます。
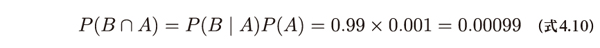
病気であるが検査結果が陰性となる確率は、単純な引き算で次のように計算することができます。
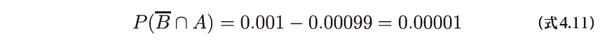
また、問題文の中では病気でない場合に陽性の検査結果が出る確率が与えられています。これは次のような条件付き確率です。
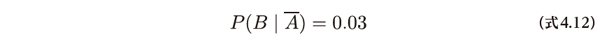
同時確率のP(A∩B)かP(A∩B)のどちらかが求まればP(B)を計算できます。(式4.1)をもとに、病気でなく検査が陽性である場合の同時確率P(A∩B)は次のように求められます。
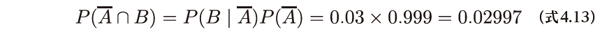
(式4.10)と(式4.13)から検査結果が陽性である周辺確率P(B)が求まります。
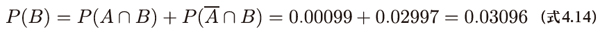
以上の計算結果を用いて、陽性の検査結果の場合に病気に罹患している確率P(A|B)は次のように推定できます。
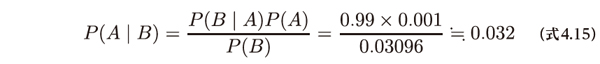
つまり、検査を受けて陽性反応であった場合、その人が病気である確率は3.2%ということがわかりました。99%の感度の検査をしたのに3.2%は意外と小さいと感じるかもしれません。これは病気の人は稀で、健康な人の方がずっと多い中での検査だったためです。健康な人でも3%の誤った反応が出るので、そのケースが無視できないほど大きい数値だったということです。
しかし、病気である確率は何も検査をしないと0.1%でした。検査によって陽性反応が観測されることで、病気である確率が3.2%に上がりました。32倍の変化であり、このまま問題なしといえるわけではないので注意してください。
ここで、ベイズの定理の式の中の数式について少し考えてみましょう。まずはベイズの定理の(式4.5)の左辺にあるP(A|B)と右辺にあるP(B|A)に注目してみてください。これはAとBの位置が逆です。ベイズの定理の「Bが発生した前提でAが発生する確率」は、逆の「Aが発生した前提でBが発生する確率」から計算できることを意味しています。片方の条件付き確率は、もう一方のものよりも簡単に求めることができる場合があります。
この例題では「検査が陽性であった場合に病気である確率」を、逆の「病気であった場合に検査が陽性になる確率」から計算しました。この逆の条件付き確率は逆確率(inverse probability)と呼ばれます。以上のように、ベイズの定理は2つの事象に関する確率P(A|B)と、その逆確率であるP(B|A)を関係付ける定理といえます。
次に式の左辺にあるP(A|B)と右辺にあるP(A)に注目してみてください。P(A)は日本国内の患者の割合、つまり検査を受ける前に病気である確率を表しています(図4.2)。
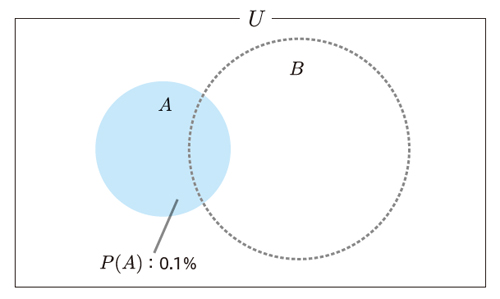
P(A|B)は検査を受けて陽性反応であった場合に、その人が病気である確率を表しています。これは陽性である事象Bを全体と考え、その中である人が病気である確率をベイズの定理を使って再計算したことになります(図4.3)。
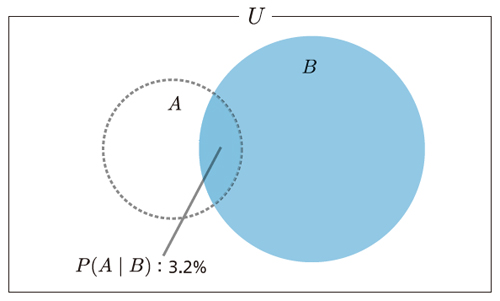
このP(A)を事前確率(prior probability)、P(A|B)を事後確率(posterior probability)と呼びます。事後確率は逆確率の別名でもあります。
この例における検査を受けるということは、データを収集する、観測するということです。ベイズの定理は、観測を通じて事前確率をもとに事後確率を計算するための式といえます。今回の例題では、検査で陽性反応が出たという観測結果から、病気に罹患している確率を計算しました。




